Tutorial • RaCE.NMA

Overview

In this vignette, we provide a detailed tutorial of the key functionalities of the RaCE.NMA R package. The package has functions to complete three primary tasks when utilizing the proposed RaCE methodology for network meta-analysis:

Model estimation
Model assessment
Inference and summary statistics

We demonstrate each of these tasks below, after loading the necessary packages.

library(RaCE.NMA)
library(reshape2) # data reformatting
library(ggplot2)  # creating nice figures

Data

Throughout this tutorial, we use a dataset displaying the results of a previous NMA study provided by Wang et. al (2022). The data is loaded below:

data("WangPosteriors")
wang_posterior <- mcmc.df[,4:13] # posteriors of non-baseline treatments
wang_ybar <- c(0, apply(wang_posterior,2,mean)) # calculating mean relative treatment effects
wang_cov <- cov(wang_posterior) # calculating covariance of relative treatment effects
wang_cov <- cbind(c(min(apply(wang_posterior,2,var))/10, rep(0,10)), # updating covariance for baseline treatments
             rbind(0,wang_cov) )
wang_s <- sqrt(diag(wang_cov))
treatments <- c("R-CHOP","R-CHOP-R","R-Benda","R-Benda-R","R-Benda-R4",
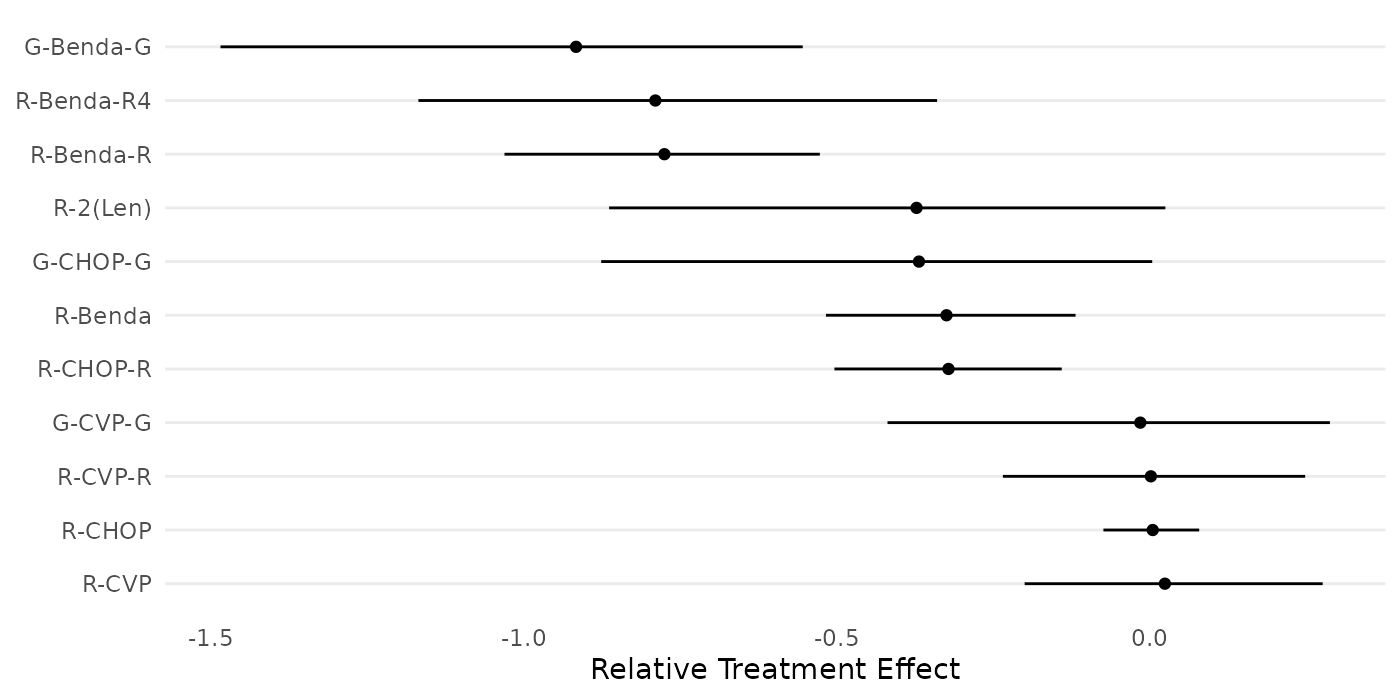
              "R-CVP","R-CVP-R","R-2(Len)","G-CVP-G","G-CHOP-G","G-Benda-G")

The following forest plot displays the relative treatment effects of the 11 treatments in the study, as estimated by Wang et. al (2022).

forestplot_data <- data.frame(
  name=treatments, 
  mean=wang_ybar,
  lower_CI=c(-1.96*sqrt(min(apply(wang_posterior,2,var))/10),apply(wang_posterior,2,function(x){quantile(x,0.025)})),
  upper_CI=c(1.96*sqrt(min(apply(wang_posterior,2,var))/10),apply(wang_posterior,2,function(x){quantile(x,0.975)}))
)[-1,] # excluding baseline treatment
forestplot_data$name <- factor(forestplot_data$name,levels=forestplot_data$name[order(forestplot_data$mean)])
ggplot(forestplot_data, aes(y=name, x=mean, xmin=lower_CI, xmax=upper_CI) ) +
  geom_point() + geom_linerange() +
  scale_y_discrete(limits=rev) + labs(y="Treatment",x="Posterior") + 
  theme_bw() + theme(panel.grid.minor = element_blank(),panel.grid.major.x = element_blank())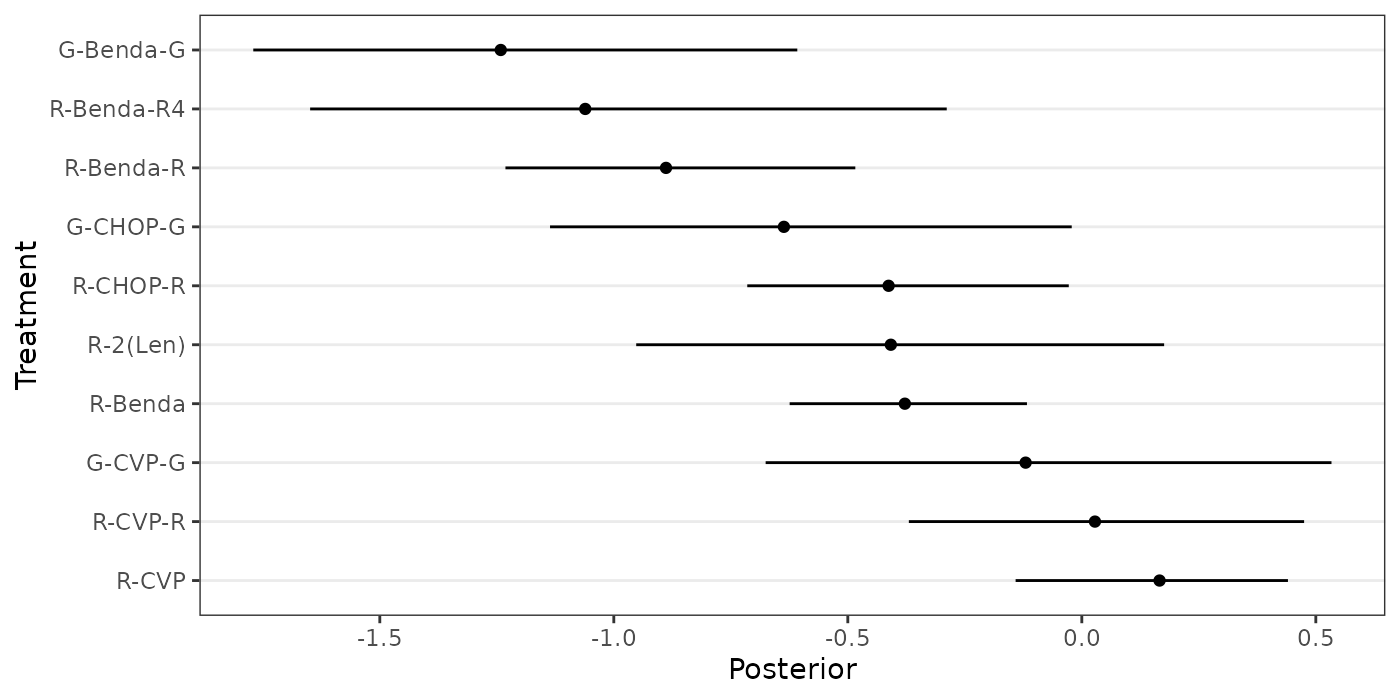

1. Model Estimation

The RaCE.NMA packages contains a primary model-fitting function, mcmc_RCMVN. The function requires many inputs, which may be broken down into three categories:

Previous results from an NMA analysis: The user must provide results on the relative treatment effects from a previous NMA study. Various formats are allowed; see below.
Model hyperparameters: Parameters which correspond to “priors” in the Bayesian model. Vague priors are available by default.
MCMC settings: Specifications of an MCMC estimation procedure, including the number of independent chains, length of each chain, thinning and burn-in, etc. By default, the function runs 2 chains, each of length 15000 and removes the first half of iterations as burn-in.

Previous results from an NMA analysis

If available, we recommend inputting the full posterior of the relative treatment effect from a previous NMA analysis into the mcmc_RCMVN function. In this case, the posterior argument should be provided an $N\times J$ matrix, where the (i,j) entry indicates the relative treatment effect of treatment $j$ in MCMC draw $i$ . An example of this functionality is provided below:

mcmc_RCMVN(posterior = wang_posterior)

In the above code, default settings are used for all other inputs. (We recommend against this practice.)

Alternatively, one may provide summary statistics of the model posterior (instead of a full posterior itself). This is useful when applying the RaCE-NMA methodology to the results of a published paper post-hoc, when only summary statistics are available. In this setting, the user must provide two inputs:

ybar: A vector of length $J$ (the number of treatments), where the $j$ th entry displays the average relative treatment effect of treatment $j$
cov or s: A $J\times J$ matrix or vector of length $J$ , which contain either a covariance matrix of the relative treatment effects or the treatment-specific standard deviations of relative treatment effects.

If posterior is provided, any inputs for ybar, cov, and s will be ignored. If cov is provided, s is ignored. An example of this functionality is provided below:

mcmc_RCMVN(ybar = wang_ybar, cov = wang_cov) # cov example
mcmc_RCMVN(ybar = wang_ybar, s = wang_s) # s example

Model hyperparameters

Next, we may specify the following hyperparameters:

mu0: The prior mean on the rank-clustered relative treatment effects. Defaults to mean(ybar), which aims to be vague.
sigma0: The prior standard deviation on the rank-clustered relative treatment effects. Defaults to sqrt(10*var(ybar)), which aims to be vague.

The following code demonstrates how one could specify these hyperparameters directly in the estimation function:

mcmc_RCMVN(posterior = wang_posterior, 
           mu0 = mean(wang_ybar), sigma0 = sqrt(10*var(wang_ybar)) )

MCMC settings

Last, we may specify parameters that control how the MCMC chains are run:

tau: The standard deviation of the Metropolis Hastings proposal distribution. Defaults to min(|ybar_i-ybar_j|).
nu0: How cluster-specific mean parameters are initialized. Defaults to NULL, which randomly samples from the prior distribution.
num_iters: The number of times the rank-clustering structure is sampled in each MCMC chain. Defaults to $5{,}000$ .
nu_reps: The number of times each cluster-specific mean is sampled per sampling of the rank-clustering structure. Defalts to $3$ . In total, there will be num_iters $\times$ nu_reps samples from the posterior.
chains: The number of independent MCMC chains. Defaults to 2.
burn_prop: The proportion of MCMC samples in each chain to be removed as burn-in. Defaults to 0.5.
thin: A number indicating how often to thin samples. Defaults to 1, indicating no thinning.
seed: The random seed to run chains. Defaults to NULL, meaning the environment seed is inherited.

The following code demonstrates how one could specify some of these settings directly in the estimation function:

mcmc_results <- mcmc_RCMVN(
  ybar = wang_ybar, cov = wang_cov,
  mu0 = mean(wang_ybar), sigma0 = sqrt(10*var(wang_ybar)),
  num_iters = 10000, nu_reps = 2, chains = 2, seed = 1 
)
#> [1] "Estimating chain 1 of 2."
#> [1] "Estimating chain 2 of 2."

2. Model Assessment

The package contains three functions to assess if the MCMC chains have converged and mixed. The first two produce trace plots of mu and K, the primary model parameters. The third calculates the $\hat{R}$ statistic for each mu parameter. A standard rule of thumb is to ensure that $\hat{R}<1.1$ .

createtrace_mu(mcmc_results, names=treatments)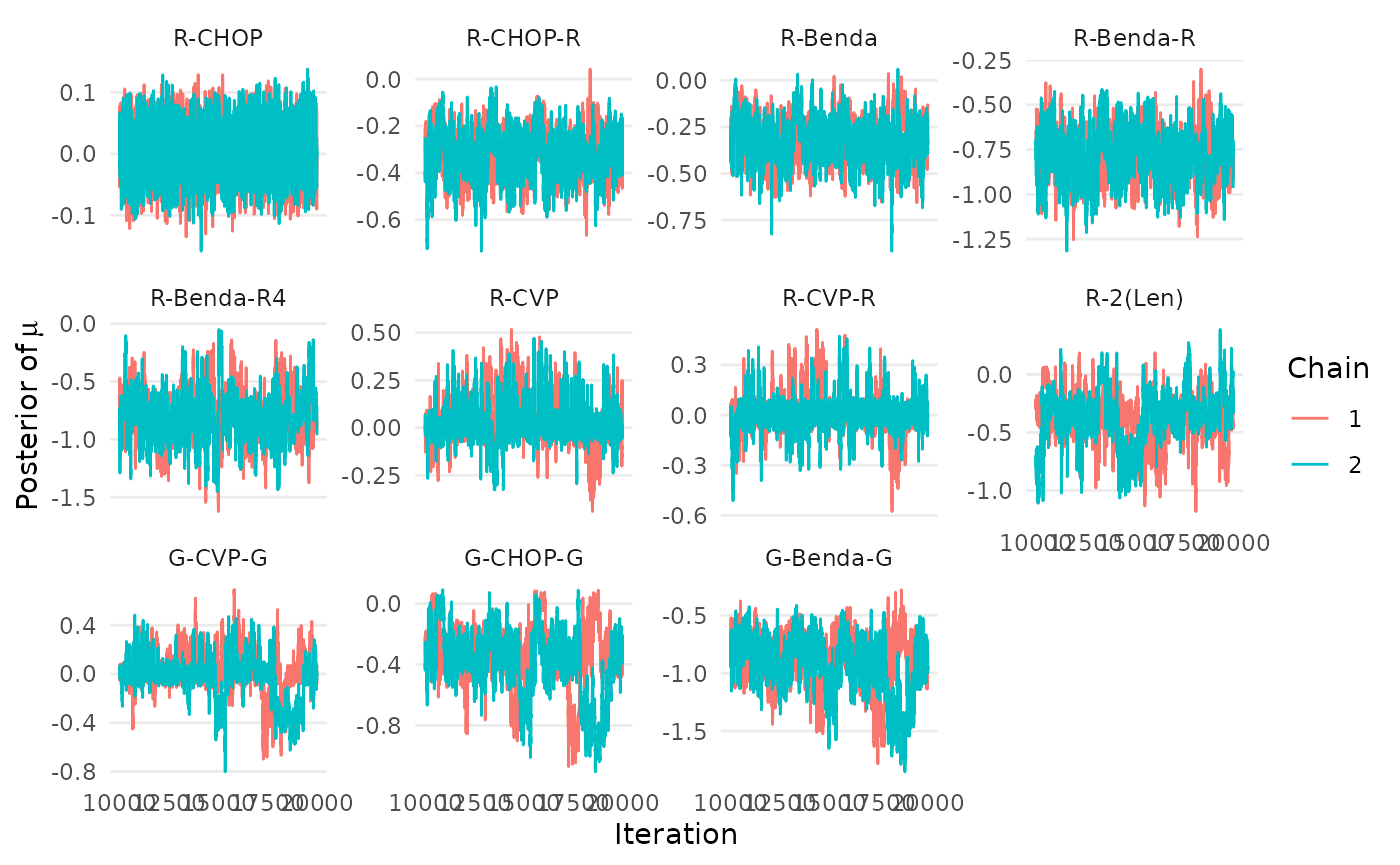

createtrace_K(mcmc_results)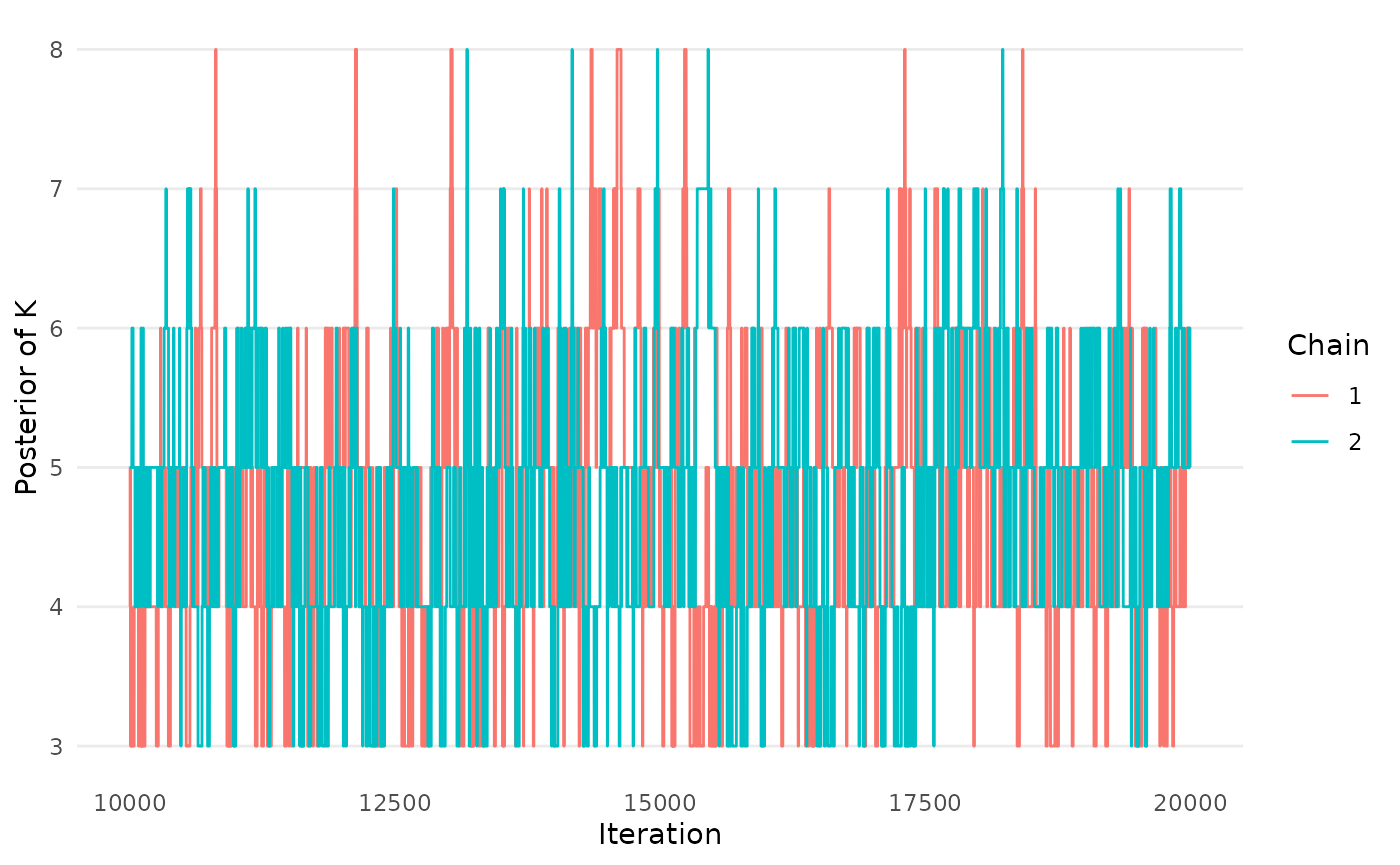

calculate_Rhat(mcmc_results, names=treatments)
#> Potential scale reduction factors:
#> 
#>            Point est. Upper C.I.
#> R-CHOP           1.00       1.01
#> R-CHOP-R         1.01       1.06
#> R-Benda          1.02       1.09
#> R-Benda-R        1.00       1.02
#> R-Benda-R4       1.00       1.00
#> R-CVP            1.08       1.30
#> R-CVP-R          1.09       1.32
#> R-2(Len)         1.16       1.55
#> G-CVP-G          1.08       1.31
#> G-CHOP-G         1.19       1.65
#> G-Benda-G        1.16       1.55

3. Inference and summary statistics

Often, we are most interested in creating a clustering probability matrix and a cumulative ranking curve. We create these plots in the code chunks below.

create_clustermatrix(mcmc_results, names = treatments, label_ranks = 1)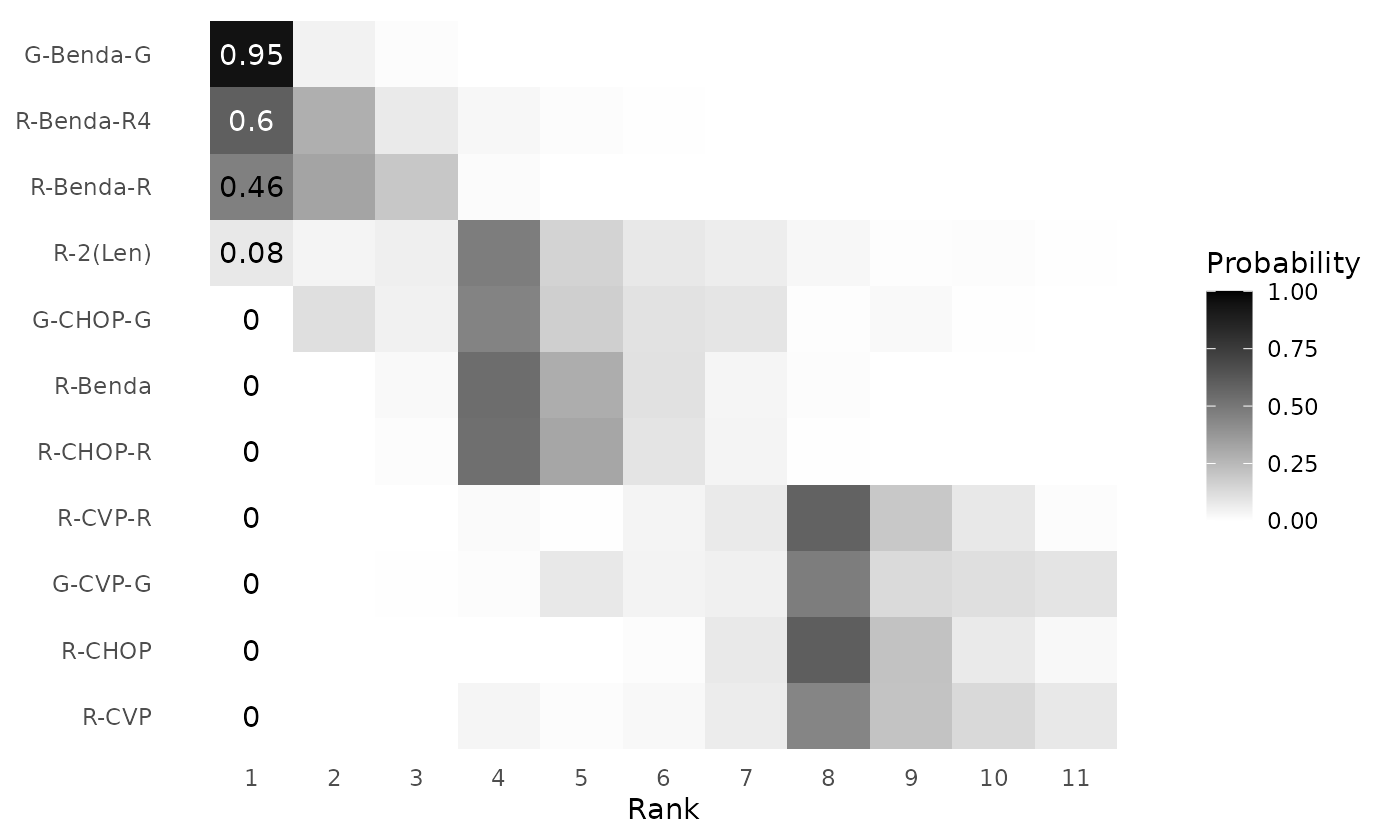

create_cumulativeranking(mcmc_results, names=treatments)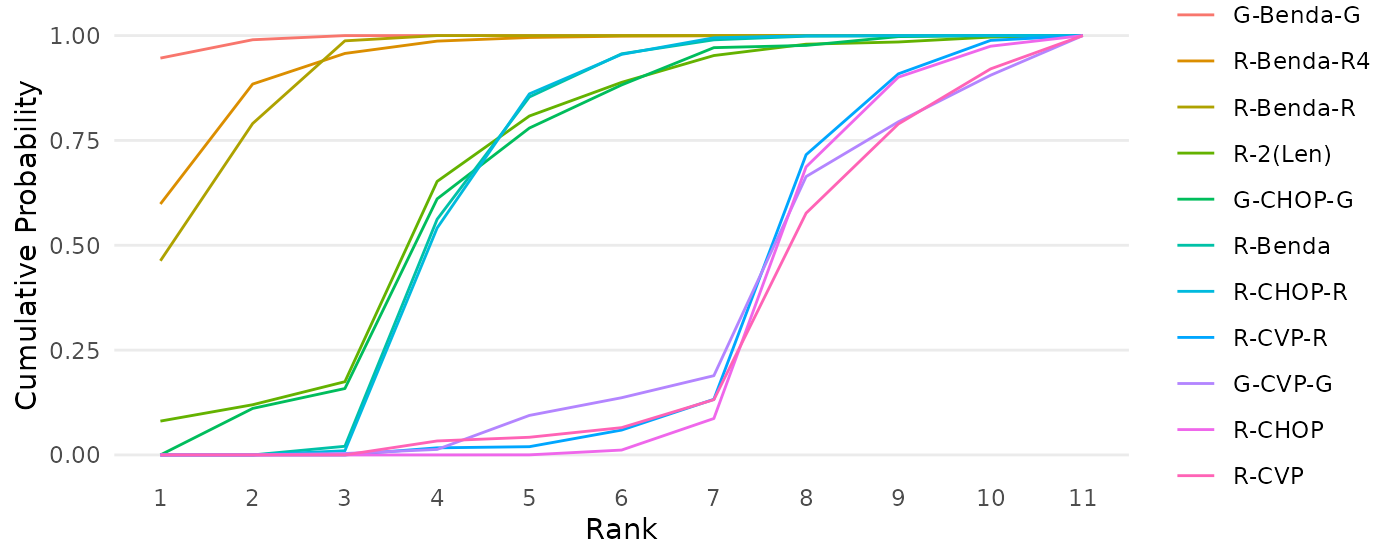

The package also includes functions to produce violin plots of model posteriors.

create_violinplot(mcmc_results,names=treatments)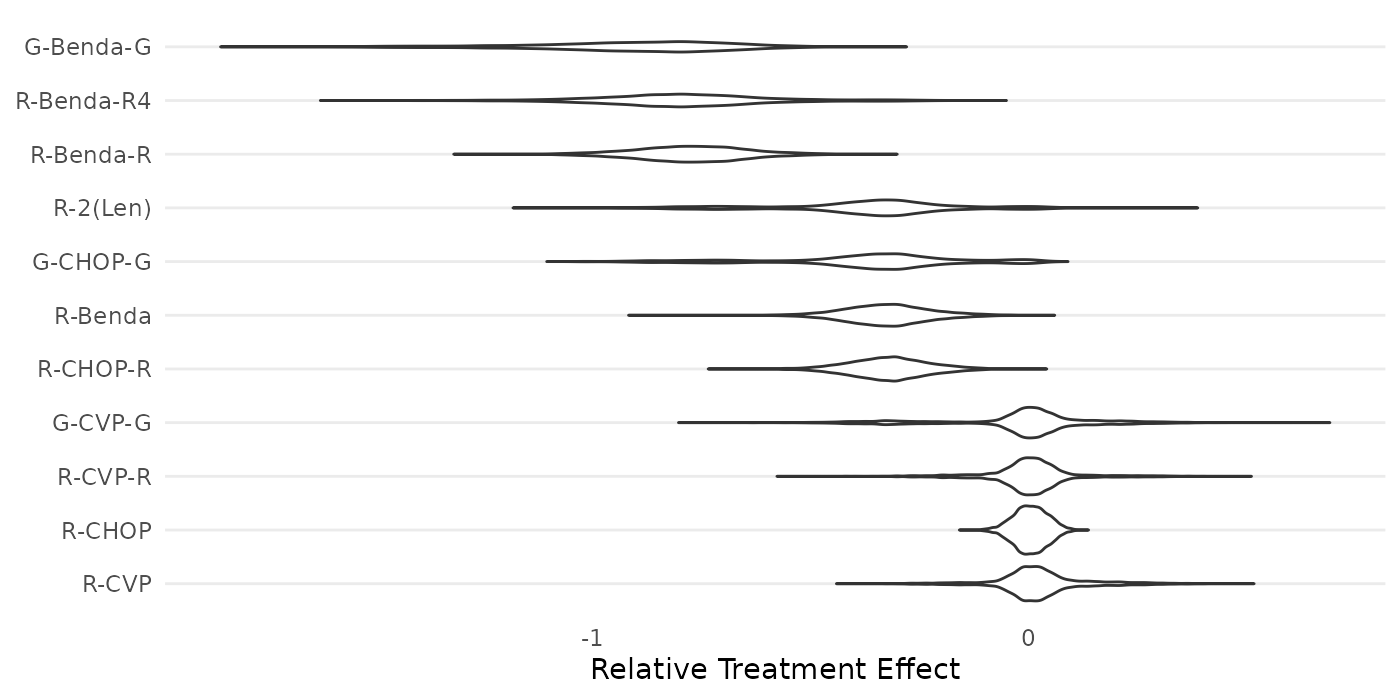

create_forestplot(mcmc_results,names=treatments)